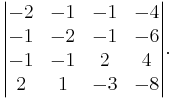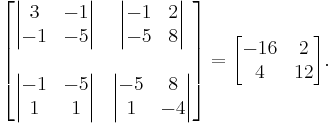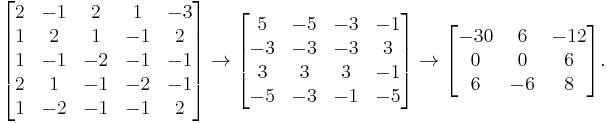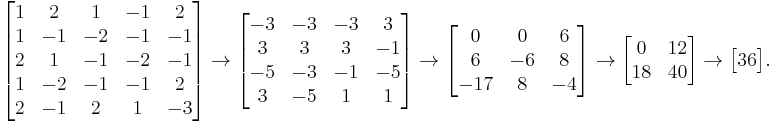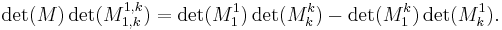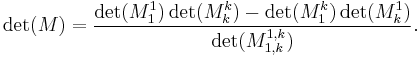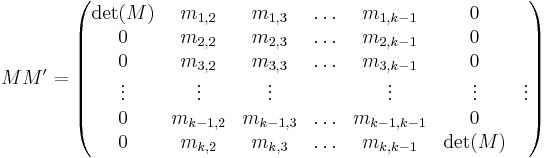Dodgson condensation
In mathematics, Dodgson condensation is a method of computing the determinants of square matrices. It is named for its inventor Charles Dodgson (better known as Lewis Carroll). The method in the case of an n × n matrix is to construct an (n − 1) × (n − 1)matrix, an (n − 2) × (n − 2), and so on, finishing with a 1 × 1 matrix, which has one entry, the determinant of the original matrix.
Contents |
The General Method
This algorithm can be described in the following 4 steps:
- Let A be the given n × n matrix. Arrange A so that no zeros occur in its interior. An explicit definition of interior would be all ai,j with
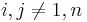 . We can do this using any operation that we could normally perform without changing the value of the determinant, such as adding a multiple of one row to another.
. We can do this using any operation that we could normally perform without changing the value of the determinant, such as adding a multiple of one row to another. - Create an (n − 1) × (n − 1) matrix B, consisting of the determinants of every 2 × 2 submatrix of A. Explicitly, we write
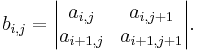
- Using this (n − 1) × (n − 1) matrix, perform step 2 to obtain an (n − 2) × (n − 2) matrix C. Divide each term in C by the corresponding term in the interior of A.
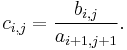
- Let A = B, and B = C. Repeat step 3 as necessary until the 1 × 1 matrix is found; its only entry is the determinant.
Examples
Without Zeros
We wish to find
We make a matrix of its 2 × 2 submatrices.
We then find another matrix of determinants:
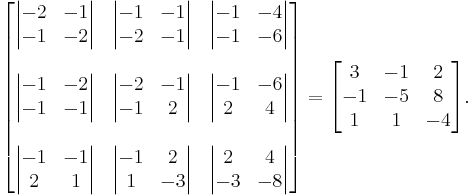
We must then divide each element by the corresponding element of our original matrix. The interior of our original matrix is 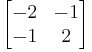 , so after dividing we get
, so after dividing we get 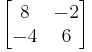 . The process must be repeated to arrive at a 1 × 1 matrix.
. The process must be repeated to arrive at a 1 × 1 matrix. 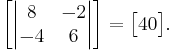 We divide by the interior of our 3 × 3 matrix, which is just -5, giving us
We divide by the interior of our 3 × 3 matrix, which is just -5, giving us 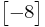 . -8 is indeed the determinant of the original matrix.
. -8 is indeed the determinant of the original matrix.
With Zeros
Simply writing out the matrices:
Here we run into trouble. If we continue the process, we will eventually be dividing by 0. We can perform four row exchanges on the initial matrix to preserve the determinant and repeat the process, with most of the determinants precalculated:
Hence, we arrive at a determinant of 36.
The Desnanot-Jacobi identity and proof of correctness of the condensation algorithm
The proof that the condensation method computes the determinant of the matrix if no divisions by zero are encountered is based on an identity known as the Desnanot-Jacobi identity.
Let 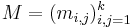 be a square matrix, and for each
be a square matrix, and for each 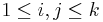 denote by
denote by 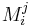 the matrix that results from
the matrix that results from  by deleting the
by deleting the  -th row and the
-th row and the  -th column. Similarly, for
-th column. Similarly, for 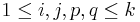 denote by
denote by 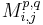 the matrix that results from
the matrix that results from  by deleting the
by deleting the  -th and
-th and  -th rows and the
-th rows and the  -th and
-th and  -th columns.
-th columns.
The Desnanot-Jacobi identity
Proof of the correctness of Dodgson condensation
Rewrite the identity as
Now note that by induction it follows that when applying the Dodgson condensation procedure to a square matrix  of order
of order  , the matrix in the
, the matrix in the  -th stage of the computation (where the first stage
-th stage of the computation (where the first stage 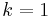 corresponds to the matrix
corresponds to the matrix  itself) consists of all the connected minors of order
itself) consists of all the connected minors of order  of
of  , where a connected minor is the determinant of a connected
, where a connected minor is the determinant of a connected 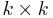 sub-block of adjacent entries of
sub-block of adjacent entries of  . In particular, in the last stage
. In particular, in the last stage 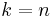 we get a matrix containing a single element equal to the unique connected minor of order
we get a matrix containing a single element equal to the unique connected minor of order  , namely the determinant of
, namely the determinant of  .
.
Proof of the Desnanot-Jacobi identity
We follow the treatment in Bressoud's book; for an alternative combinatorial proof see the paper by Zeilberger. Denote 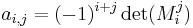 (up to sign, the
(up to sign, the 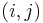 -th minor of
-th minor of  ), and define a
), and define a 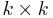 matrix
matrix 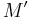 by
by
(Note that the first and last column of 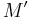 are equal to those of the adjugate matrix of
are equal to those of the adjugate matrix of  ). The identity is now obtained by computing
). The identity is now obtained by computing 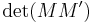 in two ways. First, we can directly compute the matrix product
in two ways. First, we can directly compute the matrix product 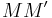 (using simple properties of the adjugate matrix, or alternatively using the formula for the expansion of a matrix determinant in terms of a row or a column) to arrive at
(using simple properties of the adjugate matrix, or alternatively using the formula for the expansion of a matrix determinant in terms of a row or a column) to arrive at
where we use 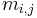 to denote the
to denote the 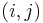 -th entry of
-th entry of  . The determinant of this matrix is
. The determinant of this matrix is 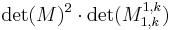 .
.
Second, this is equal to the product of the determinants, 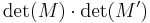 . But clearly
. But clearly
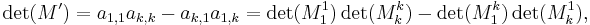
so the identity follows from equating the two expressions we obtained for 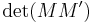 and dividing out by
and dividing out by 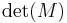 (this is allowed if one thinks of the identities as polynomial identities over the ring of polynomials in the
(this is allowed if one thinks of the identities as polynomial identities over the ring of polynomials in the 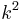 indeterminate variables
indeterminate variables 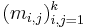 ).
).
References and further reading
- Condensation of Determinants, Being a New and Brief Method for Computing their Arithmetical Values, by C. L. Dodgson
Proceedings of the Royal Society of London © 1866 The Royal Society
- Bressoud, David M., Proofs and Confirmations: The Story of the Alternating Sign Matrix Conjecture, MAA Spectrum, Mathematical Associations of America, Washington, D.C., 1999.
- Bressoud, David M. and Propp, James, How the alternating sign matrix conjecture was solved, Notices of the American Mathematical Society, 46 (1999), 637-646.
- Knuth, D. (1996) Overlapping Pfaffians, Electronic Journal of Combinatorics 3 no. 2.
- Mills, William H., Robbins, David P., and Rumsey, Howard, Jr., Proof of the Macdonald conjecture, Inventiones Mathematicae, 66 (1982), 73-87.
- Mills, William H., Robbins, David P., and Rumsey, Howard, Jr., Alternating sign matrices and descending plane partitions, Journal of Combinatorial Theory, Series A, 34 (1983), 340-359.
- Robbins, David P., The story of
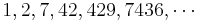 , The Mathematical Intelligencer, 13 (1991), 12-19.
, The Mathematical Intelligencer, 13 (1991), 12-19. - Zeilberger, D., Dodgson's determinant evaluation rule proved by two-timing men and women. Elec. J. Comb. 4 (1997).
External links
- Dodgson Condensation entry in MathWorld